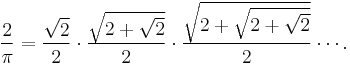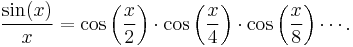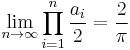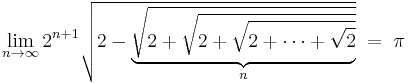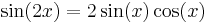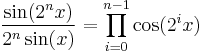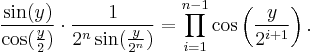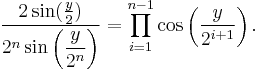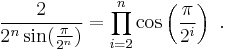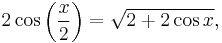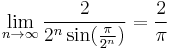Viète's formula

This article is not about Viète's formulas for symmetric polynomials.

In mathematics, the Viète formula, named after François Viète (1540–1603), is the following infinite product representating the mathematical constant π:

$\frac2\pi= \frac{\sqrt2}2\cdot \frac{\sqrt{2%2B\sqrt2}}2\cdot \frac{\sqrt{2%2B\sqrt{2%2B\sqrt2}}}2\cdots.$

The above formula is now considered as a result of one of Leonhard Euler's formula – branded more than one century later. Euler discovered that:

$\frac{\sin(x)}x=\cos\left(\frac{x}2\right)\cdot\cos\left(\frac{x}4\right)\cdot\cos\left(\frac{x}8\right)\cdots.$

Substituting x = π/2 will produce the formula for 2/π, that is represented in an elegant manner by Viète.

The expression on the right hand side has to be understood as a limit expression

$\lim_{n \rightarrow \infty} \prod_{i=1}^n {a_i \over 2}=\frac2\pi$

where a_n = √2 + a_{n − 1}, with initial condition a₁ = √2 (Wells 1986, p. 50; Beckmann 1989, p. 95). However, this expression was not rigorously proved to converge until Rudio (1892).

Upon simplification, a beautiful formula of π is given by

$\lim_{n\to\infty}2^{n %2B1}\sqrt{2-\underbrace{\sqrt{2%2B\sqrt{2%2B\sqrt{2%2B\cdots%2B\sqrt{2}}}}}_{n}}\;=\;\pi$

Proof

Using an iterated application of the double-angle formula

$\, \sin(2x)=2\sin(x)\cos(x)$

for sine one first proves the identity

${{\sin(2^n x)}\over {2^n \sin(x)}}=\prod_{i=0}^{n-1} \cos(2^i x)$

valid for all positive integers n. Letting x = y/2ⁿ and dividing both sides by cos(y/2) yields

${{\sin( y)}\over {\cos({y\over 2} )}}\cdot{1\over {2^n \sin({y\over {2^n}})}}=\prod_{i=1}^{n-1} \cos\left({y\over {2^{i%2B1}}}\right).$

Using the double-angle formula siny = 2sin(y/2)cos(y/2) again gives

${{2\sin({y\over 2})}\over {2^n \sin\left(\displaystyle{y\over {2^n}}\right)}}=\prod_{i=1}^{n-1} \cos\left({y\over {2^{i%2B1}}}\right).$

Substituting y = π gives the identity

${2\over {2^n \sin({\pi \over {2^n}})}}=\prod_{i=2}^{n} \cos\left({\pi\over {2^i}} \right) \ .$

It remains to match the factors on the right-hand side of this identity with the terms a_n. Using the half-angle formula for cosine,

$2\cos\left({x \over 2}\right)=\sqrt{2%2B2\cos x},$

one derives that b_i = 2cos(π/2^{i + 1}) satisfies the recursion b_{i + 1} = √2 + b_i with initial condition b₁ = 2cos(π/4) = √2 = a₁. Thus a_n = b_n for all positive integers n.

The Viète formula now follows by taking the limit n → ∞. Note here that

$\lim_{n \rightarrow \infty} {2\over {2^n \sin({\pi \over {2^n}})}}={2\over \pi}$

as a consequence of the fact that lim_{x → 0}sin(x)/x = 1. (This limit is the derivative of sinx at x = 0, that is cos(0) = 1.)